多因一效、一因多效、各效相等(?),多基因形状
定义: 基因型值(G):某基因型对性状数值造成的影响,包括等位基因间的加性(A)、显性效应(D)和非等位基因间的上位效应(I) 满足
G=A+D+I
根据多基因学说,一对等位基因间的基因型值可以如下图给出:
 表型值(P):个体某性状实际测量到的数值,包括基因型值(P)与环境效应(E) 满足
表型值(P):个体某性状实际测量到的数值,包括基因型值(P)与环境效应(E) 满足
P=G+E
一般地,在育种工作中,由于基因型的纯合化,显性效应将逐渐消失,而上位效应则过于复杂,一般不予分析,通常将显性、上位以及环境影响归入一起,称剩余值(R) 有
R=D+I+E
而将加性方差称为育种值 考察一个足够大的群体,总表型值满足
ΣP=ΣG+ΣE
因为群体足够大,各有正负的环境效应相互抵消 满足
ΣE=0
故
P=G
即群体平均表型值等于群体平均基因型值 这告诉我们全群性状的平均值往往反映了全群该性状的遗传水平
但在任何一个群体中,个体与个体之间均不可避免的存在差异 我们往往希望知道个体之间的差异是由什么原因导致的,即能够定量地分析遗传效应与环境效应对于个体间的差异各自占多大的影响 首先我们要量化群体中个体间差异的程度,通常使用方差(σ2) 对于大小已知、各个体均充分了解的整个群体,有:
σ2=ΣfΣf(x−x)2=Σfx2−Σ(fx)2
式中f为各基因型个体占比,有Σf=1,该式子具体推导不难请自行证明
接着,我们引入遗传率(heritability) 广义遗传率(h)被定义为遗传方差(VG)与表型方差(VP)的比值:
h=VPVG
狭义遗传率(H)被定义为加性方差(VA)与表型方差(VP)的比值:
H=VPVA
与生物适应型关系低的形状其遗传率往往较高,如人的指纹总嵴数可高达97%
以一对等位基因,A1A1×A2A2为例 亲代平均基因型值分别为a与−aF1基因型值为d 对于F2代基因型值,有: 由前述方差计算公式带入 有
由前述方差计算公式带入 有
σG2=Σfx2−Σ(fx)2=21a2+41d2
如果有n对互不连锁、控制统一性状的基因,其作用具有可加性:
VG=21Σa2+41Σd2
令加性方差:VA=Σa2 显性离差:VD=Σd2 则
VG=21VA+41VD
显然:
VP=21VA+41VG+VE
我们知道,一致性群体(纯合体)不存在VG,因此使用31(VP1+VP2+VF1)估计VE 进而可以计算VG与H
对于狭义遗传率,则需要借助F1分别与两亲本回交产生的B1与B2

VB1=21(a2+d2)−41(a+d)2+VE=41(a2−2ad+d2)+VE
VB2=21(a2+d2)−41(d−a)2+VE=41(a2+2ad+d2)+VE
因此:
21(VB1+VB2)=41VA+41VD+VE
进而可计算h与平均显性程度
ad=VAVD
类似上面所做的计算再结合一些统计学推导可以知道:
h2=rArP1P2
其中: rP1P2表示亲属1与亲属2间该性状表型的相关系数rA表示亲属1与亲属2的亲缘系数(遗传相关系数)
如亲代(P)与子女(O)间:h2=0.5+0.5rOP=rOP 注意:
- 考虑亲代子代之间时应当抽象为亲代是一“个体”,它的自交产生了子代(即子代所有遗传物质均来自于亲代,亲子代间亲缘系数应当为1)
- 这样理解的含义是单独父本或母本与后代的亲缘系数是0.5,但亲本整体与后代的亲缘系数是1
由回归系数(斜率) 的最小二乘估计:
b=SSa⋅SSbSSab
与相关系数:rOP=SSpSSop比较,可以得到在群体标准差一致或子代生长群体平均值已知时有
SSa=N⋅σa2=N⋅σb2=SSb↔r=b
因此:
h2=rArP1P2=rOP=bOP
其中PM代表双亲中值,用T表示表型值,则有:
TPM=21(TP1+TP2)
进而:
TO=μ+h2(TPM−μ)
或:
[TO−μ]=h2[TPM−μ]
注意:照应上文,此处所使用的亲代值为双亲平均,而非单独的父本或母本,如果单独使用父本或母本,h2应当等于2倍父本或母本与后代间的相关系数,所得公式应当是
[TO−μ]=21×h2[TFa/Mo−μ]
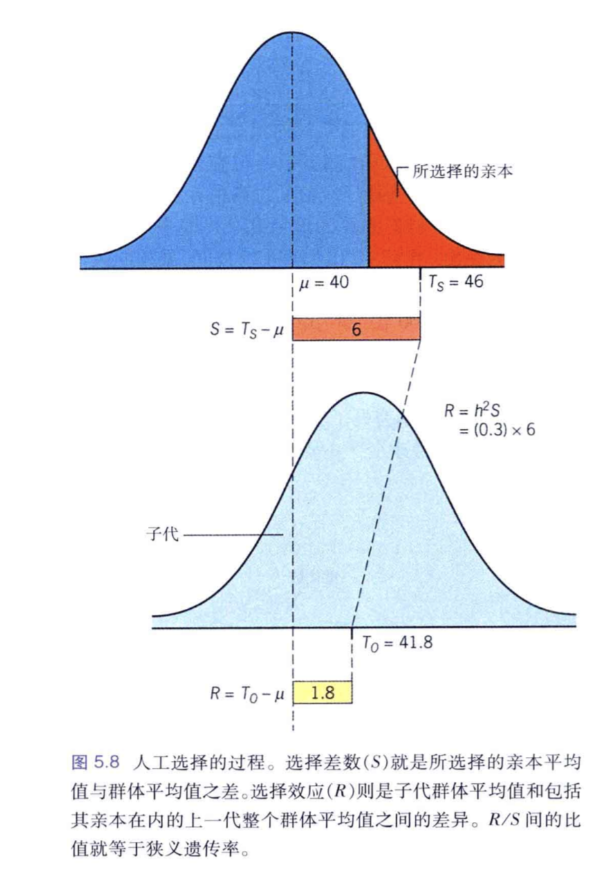
在一个亲本不变,指定另一亲本(PS)或选定一定表型亲本(PS)互相交配时,则有:
[TO−μ]=h2[TPS−μ]
上述公式允许我们在生长群体平均值已知(提供环境效应的信息)、亲本平均值已知(提供遗传效应的信息)的情况下根据遗传率预测子代的表型平均值 例如: 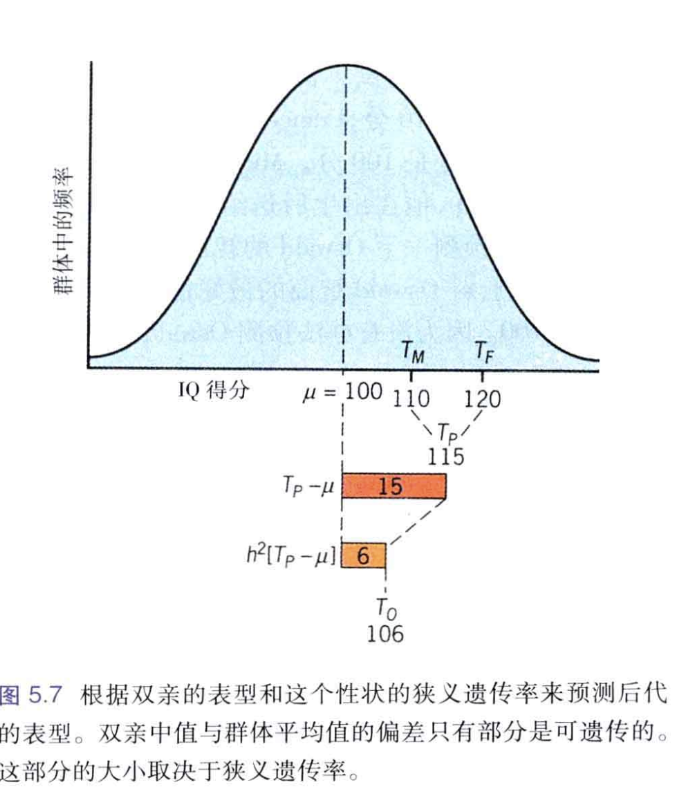
 表型值(P):个体某性状实际测量到的数值,包括基因型值(P)与环境效应(E) 满足
表型值(P):个体某性状实际测量到的数值,包括基因型值(P)与环境效应(E) 满足 由前述方差计算公式带入 有
由前述方差计算公式带入 有


